JEE 2013 :: Advanced 2013 :: Mathematics 2013

• Advanced 2013 - Physics 2013
• Advanced 2013 - Chemistry 2013
• Advanced 2013 - Mathematics 2013

A pack contains n card numbered from 1 to n . Two consecutive numbered card are removed from the pack and the sum of the numbers on the remaining cards is 1224. If the smaller of the numbers on the removed cards is k, then k-20 is equal to 

Answer:

Explanation:

Let number of removed cards  are k and (k+1)

 $\therefore$    $\frac{n(n+1)}{2}-k-(k+1)=1224$

 $\Rightarrow$    n²+n-4k=2450

$\Rightarrow$    n²+n-2450=4k

$\Rightarrow$   (n+50)(n-49)=4k

$\therefore$   n>49   let n=50

$\therefore$  100=4k, k=25

$\Rightarrow$  k-20=5

Of the three independent events  $E_{1},E_{2} and E_{3}$  , the probability that only $E_{1}$ occurs is $\alpha$ , only $E_{2}$ occurs is β   and only $E_{3}$ occurs is $\gamma$ .Let  the probability p that none  of $E_{1}$ , $E_{2}$ or $E_{3}$ occurs satisfy the equations   $(\alpha-2\beta),p=\alpha\beta$ and   $ (\beta-3\gamma)$   $ p=2\beta\gamma$  .All the given probabilities are assumed to lie in the interval (0,1)

 Then, probability of occurrence of E₁/ probability of occurrence  of E₃ is equal to

Answer:

Explanation:

Concept involved

 For   the events to be independent.

 $P(E_{1}\cap E_{2}\cap E_{3})=P(E_{1}) P(E_{2})P(E_{3})$

$P(E_{1}\cap \overline{E}_{2}\cap \overline{E}_{3})=P$

                                    (on;y E₁ occurs)

 =   $P(E_{1}).(1-P(E_{2}))(1-P(E_{3}))$

 let x,y,z are probability of  $E_{1}$, $E_{2}$ and $E_{3}$ respectively

 $\therefore$             $\alpha$   = x(1-y)(1-z)   ......(i)

                                 $\beta$    = (1-x).y(1-z)         ......(ii)

                                  $\gamma$  = (1-x)(1-y) z     ..........(iii)

$\Rightarrow$   p = (1-x) (1-y) (1-z)        ..........(iv)

 Given   $(\alpha-2\beta)p=\alpha\beta$ 

  and     $(\beta-3\gamma)p=2\beta\gamma$    .......(v)

 From above equations

 x=2y  and y=3 z

  $\therefore$  x=6z   =  $\frac{x}{z}=6$

Consider the set of eight vectors  $V= [a\hat{i}+b\hat{j}+c \hat{k}:a,b,c\in\left\{-1,1\right\}] $ .Three non-coplannar vectors can be chosen from  V in 2^p ways. The , p is

Answer:

Explanation:

 Concept involved

 The three vectors are coplanar if volume is zero. Now, those vectors which are along the diagonals of a cube, are non-coplannar

 Here, the four diagonals are

 OS, AQ, BR  and CP 

 Among set of eight vectors, four-vectors form body diagonals of a cube, imaging four will be parallel (unlike)  vectors.

 $\therefore$ Number of ways of selecting three vectors will be 

 $^{4}C_{3}\times 8=2^{5}=2^{p}$

         p=5

The coefficient of three consecutive terms  of  (1+x)ⁿ⁺⁵ are in the ratio 5:10:14 , then , n is equal to

Answer:

Explanation:

Let the  three consecutive terms in (1+x) ⁿ⁺⁵   be  t_r , t_r+1, t_r+2 . Having  coefficients   

$^{n+5}C_{r-1},^{n+5}C_{r}, ^{n+5}C_{r+1}$   given,  $^{n+5}C_{r-1}:^{n+5}C_{r}: ^{n+5}C_{r+1}$ =5:10:14

$\frac{^{n+5}C_{r}}{^{n+5}C_{r-1}}=\frac{10}{5}$

  and   $\frac{^{n+5}C_{r+1}}{^{n+5}C_{r}}=\frac{14}{10}$

 $\Rightarrow$    $\frac{n+5-(r-1)}{r}=2$

  and    $\frac{n-r+5}{r+1}=\frac{7}{5}$

$\Rightarrow$    n-r+6=2r

 and    5n-5r+25=7r+7

 $\Rightarrow$     n+6=3r

 and 5n+18=12 r

  $\therefore$    $\frac{n+6}{3}=\frac{5n+18}{12}$

$\Rightarrow$   4n+24=5n+18

$\Rightarrow$   n=6

A vertical line passing through the point (h,o) intersects the ellipse   $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$  at the points P and Q .Let the tangents to the ellipse at P and Q meet at the point R.If   $\triangle(h)$  = area of the $\triangle$  PQR , $\triangle_{1}= max \triangle(h)$ .   $\triangle_{2}= min_{1/2\leq h\leq1} \triangle(h)^{1/2\leq h\leq 1}$  , then 

$\frac{8}{\sqrt{5}}\triangle_{1}-8\triangle_{2}$ is equal to 

Answer:

Explanation:

Concept involved

 As to maximise or minimise area of triangle we sholud find area is terms of parametric coordinate and we second derivative test.

 Here , tangent at   $P(2\cos\theta,\sqrt{3}\sin\theta)$ is  

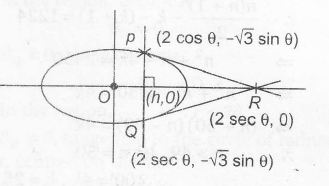
$\frac{x}{2}\cos\theta+\frac{y}{\sqrt{3}}\sin\theta=1$

 $\therefore$    $R(\sec\theta,0)$

$\Rightarrow$     $ \triangle= area of \triangle PQR$

  $=\frac{1}{2}(2\sqrt{3}\sin\theta)(2\sec\theta-2\cos\theta)$

    $=2\sqrt{3}.\sin^{3}\theta\cos\theta$   .........(i)

  Since,   $\frac{1}{2}\leq h\leq1,$

 $\therefore$      $\frac{1}{2}\leq2 cos \theta\leq1,$

    $\Rightarrow$    $\frac{1}{4}\leq cos \theta\leq\frac{1}{2}$

$\therefore$   $\frac{d\triangle}{d\theta}=\frac{2\sqrt{3}\left\{\cos\theta.3\sin^{3}\theta \cos\theta-\sin^{3}\theta(-\sin \theta)\right\}}{\cos^{2}\theta}$

    =   $\frac{2\sqrt{3}\sin^{2}\theta}{\cos^{2}\theta}[3\cos^{2}\theta+ \sin^{2}\theta]$

    =   $\frac{2\sqrt{3}\sin^{2}\theta}{\cos^{2}\theta}[2\cos^{2}\theta+ 1]$

    =  $2\sqrt{3}\tan^{2}\theta(2\cos^{2}\theta+1)>0$

   when, $\frac{1}{4}\leq \cos \theta\leq\frac{1}{2}$

$\therefore$   $\triangle_{1}=\triangle_{max}$   occurs at cos $\theta$ = $\frac{1}{4}$

=  $\left(\frac{2\sqrt{3}\sin^{3}\theta}{\cos\theta}\right)$

when   $\cos\theta=\frac{1}{4}=\frac{45\sqrt{5}}{8}$

$\triangle_{2}=\triangle_{min}$   occurs at cos $\theta$ = $\frac{1}{2}$

 =  $\left(\frac{2\sqrt{3}\sin^{3}\theta}{\cos\theta}\right)$

 when    $\cos\theta=\frac{1}{2}=\frac{9}{2}$

$\therefore$   $\frac{8}{\sqrt{5}}\triangle_{1}-8\triangle_{2}=45-36=9$

• Advanced 2013 - Physics 2013
• Advanced 2013 - Chemistry 2013
• Advanced 2013 - Mathematics 2013